Does travel distance affect results in MLS?

By Brendan Kent (@brendankent)

A key feature of Major League Soccer that differentiates it from European leagues is the physical distance between the teams. While the two-conference system reduces the average distance an away team travels for a match (teams play in-conference opponents three times per year and out-of-conference opponents once), MLS teams still spend some weeks traversing several time zones.

Back of the napkin rendering of MLS stadium locations. Obviously not perfectly to scale, but you get the drift: Western Conference teams travel farther.

In the 2013/2014 MLS Season teams traveled an average of 1,058 miles to away matches‒by this I mean the distance between the two teams’ stadiums. Houston traveled the furthest on average, at 1,345 miles per away match. The average distance traveled to away matches by each team in the 2013/2014 season is shown below. Unsurprisingly, Western Conference teams tend to travel further.

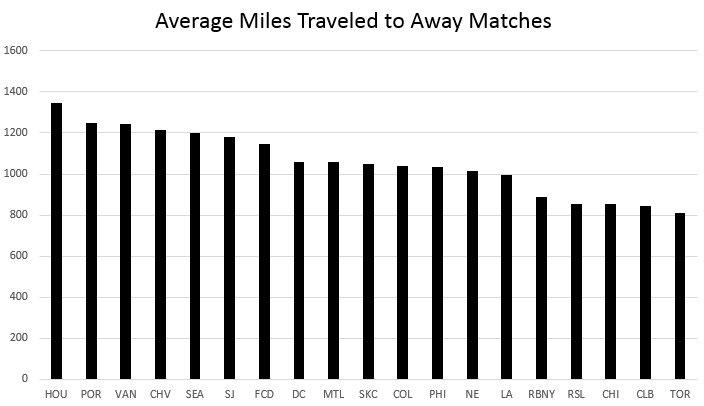
This raises the question, does travel distance effect results? In other words, can we expect teams to perform better away from home when that away match is closer to home?

In answering this question, I used multivariate regression with data from the 2013/2014 MLS regular season. Away results were used as the dependent variable to control for the significant influence of general home advantage. To control for the relative strength of the two teams, I used end of season point differential with a minor adjustment: I removed the result of the game in question to prevent any bias. I also removed any matches between LA Galaxy and Chivas USA from the data because one team was technically playing an ‘away’ game at their home stadium when they went head-to-head.

I ran several variations of the regression, all of which used away results as the dependent variable and the adjusted point differential as one of the independent variables. First, I added distance between the two teams’ stadiums as a second independent variable. This proved to be insignificant, with a p-value of .31.

Next, I ran the regression replacing distance between stadiums with the difference in time zones between the stadiums. This again proved to be an insignificant variable, returning a p-value of .5.  

Finally, I replaced the time zone variable with an indicator variable for whether the teams were two or more time zones apart. Again, insignificant, this time with a p-value of .73.

This tells us that when we control for general home advantage and the relative strengths of two teams, the physical distance between two teams has no effect on results from a statistical standpoint. This is not to say that travel takes no toll on players, it probably does, but the difference between Vancouver traveling to Portland and Vancouver traveling to New York is statistically insignificant when we control for the strength of the two teams.